《计算机视觉:模型、学习和推理》一2.4 条件概率
本文共 450 字,大约阅读时间需要 1 分钟。
2.4 条件概率
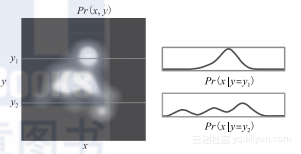
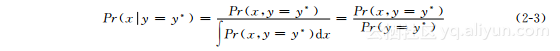
其中,使用边缘概率关系式(式(2-1))去简化分母。通常情况下不会显式定义y=y*,所以条件概率关系式可简化缩写为:
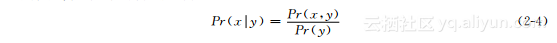 重新整理得到:
重新整理得到: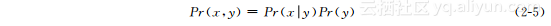 由对称性也可得:
由对称性也可得: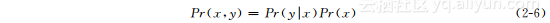 当有两个以上的变量时,可以不断用条件概率分布将联合概率分布分解为乘积形式:
当有两个以上的变量时,可以不断用条件概率分布将联合概率分布分解为乘积形式: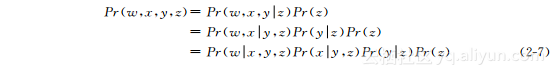
转载地址:http://vuufm.baihongyu.com/
你可能感兴趣的文章
ubuntu编译安装vim7.4
查看>>
python之利用PIL库实现页面的图片验证码及缩略图
查看>>
IP-COM设置×××
查看>>
VPC配置案例
查看>>
十年IT运维谈(五):要专业化还是平台化?
查看>>
分享超级给力的一个外发光Shader
查看>>
oblog_4.6_SQL 语句
查看>>
通过Git WebHooks+脚本实现自动更新发布代码之shell脚本
查看>>
对象实例化、字符串的使用方法
查看>>
keepalived基于LVS实现高可用,实现web服务的高可用
查看>>
80端口被Microsoft-HTTPAPI/2.0占用的解决办法
查看>>
无法抗拒Minecraft给予超高的自由度和探索-微访谈
查看>>
数据结构之串
查看>>
我的友情链接
查看>>
lvs+keepalived+nginx+tomcat高可用高性能集群部署
查看>>
实验:搭建主DNS服务器
查看>>
org.gjt.mm.mysql.Driver与com.mysql.jdbc.Driver区别
查看>>
部署exchange2010三合一:之五:功能测试
查看>>
nginx编译安装参数
查看>>
代码托管
查看>>